Ctrl+K

Advanced Indexing

Advanced Indexing#

Learning Objectives#

  • Orthogonal vs. Vectorized and Pointwise Indexing

Overview#

In the previous notebooks, we learned basic forms of indexing with xarray (positional and name based dimensions, integer and label based indexing), Datetime Indexing, and nearest neighbor lookups. In this tutorial, we will learn how Xarray indexing is different from Numpy and how to do vectorized/pointwise indexing using Xarray. First, let’s import packages needed for this repository:

import numpy as np
import pandas as pd
import xarray as xr


xr.set_options(display_expand_attrs=False)
np.set_printoptions(threshold=10, edgeitems=2)

In this notebook, we’ll use air temperature tutorial dataset from the National Center for Environmental Prediction.

ds = xr.tutorial.load_dataset("air_temperature")
da = ds.air
ds

<xarray.Dataset>
Dimensions:  (lat: 25, time: 2920, lon: 53)
Coordinates:
  * lat      (lat) float32 75.0 72.5 70.0 67.5 65.0 ... 25.0 22.5 20.0 17.5 15.0
  * lon      (lon) float32 200.0 202.5 205.0 207.5 ... 322.5 325.0 327.5 330.0
  * time     (time) datetime64[ns] 2013-01-01 ... 2014-12-31T18:00:00
Data variables:
    air      (time, lat, lon) float32 241.2 242.5 243.5 ... 296.5 296.2 295.7
Attributes: (5)

Orthogonal Indexing#

As we learned in the previous tutorial, positional indexing deviates from the behavior exhibited by NumPy when indexing with multiple arrays. However, Xarray pointwise indexing supports the indexing along multiple labeled dimensions using list-like objects similar to NumPy indexing behavior.

If you only provide integers, slices, or unlabeled arrays (array without dimension names, such as np.ndarray, list, but not DataArray()) indexing can be understood as orthogonally (i.e. along independent axes, instead of using NumPy’s broadcasting rules to vectorize indexers).

Orthogonal or outer indexing considers one-dimensional arrays in the same way as slices when deciding the output shapes. The principle of outer or orthogonal indexing is that the result mirrors the effect of independently indexing along each dimension with integer or boolean arrays, treating both the indexed and indexing arrays as one-dimensional. This method of indexing is analogous to vector indexing in programming languages like MATLAB, Fortran, and R, where each indexer component independently selects along its corresponding dimension.

For example :

da.isel(time=0, lat=[2, 4, 10, 13], lon=[1, 6, 7]).plot();  # -- orthogonal indexing
../../_images/ea2d193ea11b3615547f0c8497c6349ad9047741ed62edd2a9775ea34038b56f.png

For more flexibility, you can supply DataArray() objects as indexers. Dimensions on resultant arrays are given by the ordered union of the indexers’ dimensions:

For example, in the example below we do orthogonal indexing using DataArray() objects.

target_lat = xr.DataArray([31, 41, 42, 42], dims="degrees_north")
target_lon = xr.DataArray([200, 201, 202, 205], dims="degrees_east")

da.sel(lat=target_lat, lon=target_lon, method="nearest")  # -- orthogonal indexing

<xarray.DataArray 'air' (time: 2920, degrees_north: 4, degrees_east: 4)>
array([[[293.1    , 293.1    , 293.29   , 293.29   ],
        [284.6    , 284.6    , 284.9    , 284.19998],
        [282.79   , 282.79   , 283.19998, 282.6    ],
        [282.79   , 282.79   , 283.19998, 282.6    ]],

       [[293.19998, 293.19998, 293.9    , 294.19998],
        [283.29   , 283.29   , 285.19998, 285.19998],
        [281.4    , 281.4    , 282.79   , 283.5    ],
        [281.4    , 281.4    , 282.79   , 283.5    ]],

       ...,

       [[288.29   , 288.29   , 289.19   , 290.79   ],
        [282.09   , 282.09   , 281.59   , 282.38998],
        [280.99   , 280.99   , 280.38998, 280.59   ],
        [280.99   , 280.99   , 280.38998, 280.59   ]],

       [[289.49   , 289.49   , 290.38998, 291.59   ],
        [282.09   , 282.09   , 281.99   , 283.09   ],
        [281.38998, 281.38998, 280.59   , 280.99   ],
        [281.38998, 281.38998, 280.59   , 280.99   ]]], dtype=float32)
Coordinates:
    lat      (degrees_north) float32 30.0 40.0 42.5 42.5
    lon      (degrees_east) float32 200.0 200.0 202.5 205.0
  * time     (time) datetime64[ns] 2013-01-01 ... 2014-12-31T18:00:00
Dimensions without coordinates: degrees_north, degrees_east
Attributes: (11)

In the above example, you can see how the output shape is time x lats x lons.

But what if we would like to find the information from the nearest grid cell to a collection of specified points (for example, weather stations or tower data)?

Vectorized or Pointwise Indexing#

Like NumPy and pandas, Xarray supports indexing many array elements at once in a vectorized manner.

Vectorized indexing or Pointwise Indexing using DataArrays() can be used to extract information from the nearest grid cells of interest, for example, the nearest climate model grid cells to a collection of specified weather station latitudes and longitudes.

Hint

To trigger vectorized indexing behavior, you will need to provide the selection dimensions with a new shared output dimension name.

In the example below, the selections of the closest latitude and longitude are renamed to an output dimension named points:

# Define target latitude and longitude (where weather stations might be)
lat_points = xr.DataArray([31, 41, 42, 42], dims="points")
lon_points = xr.DataArray([200, 201, 202, 205], dims="points")
lat_points

<xarray.DataArray (points: 4)>
array([31, 41, 42, 42])
Dimensions without coordinates: points
lon_points

<xarray.DataArray (points: 4)>
array([200, 201, 202, 205])
Dimensions without coordinates: points

Now, retrieve data at the grid cells nearest to the target latitudes and longitudes (weather stations):

da.sel(lat=lat_points, lon=lon_points, method="nearest")

<xarray.DataArray 'air' (time: 2920, points: 4)>
array([[293.1    , 284.6    , 283.19998, 282.6    ],
       [293.19998, 283.29   , 282.79   , 283.5    ],
       ...,
       [288.29   , 282.09   , 280.38998, 280.59   ],
       [289.49   , 282.09   , 280.59   , 280.99   ]], dtype=float32)
Coordinates:
    lat      (points) float32 30.0 40.0 42.5 42.5
    lon      (points) float32 200.0 200.0 202.5 205.0
  * time     (time) datetime64[ns] 2013-01-01 ... 2014-12-31T18:00:00
Dimensions without coordinates: points
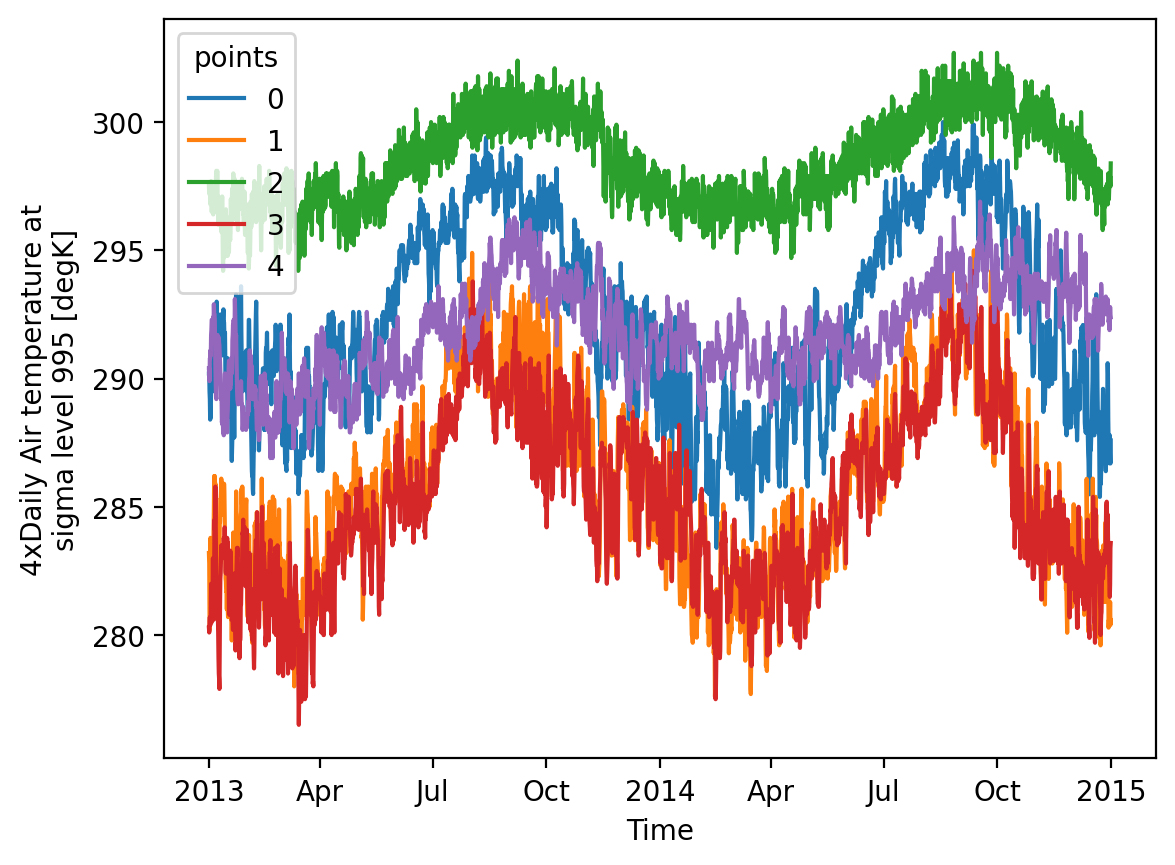
Attributes: (11)

👆 Please notice how the shape of our DataArray is time x points, extracting time series for each weather stations.

da.sel(lat=lat_points, lon=lon_points, method="nearest").dims

('time', 'points')

Attention

Please note that slices or sequences/arrays without named-dimensions are treated as if they have the same dimension which is indexed along.

For example:

da.sel(lat=[20, 30, 40], lon=lon_points, method="nearest")

<xarray.DataArray 'air' (time: 2920, lat: 3, points: 4)>
array([[[296.6    , 296.6    , 296.19998, 296.4    ],
        [293.1    , 293.1    , 293.29   , 293.29   ],
        [284.6    , 284.6    , 284.9    , 284.19998]],

       [[296.4    , 296.4    , 295.9    , 296.19998],
        [293.19998, 293.19998, 293.9    , 294.19998],
        [283.29   , 283.29   , 285.19998, 285.19998]],

       ...,

       [[293.69   , 293.69   , 293.88998, 295.38998],
        [288.29   , 288.29   , 289.19   , 290.79   ],
        [282.09   , 282.09   , 281.59   , 282.38998]],

       [[293.79   , 293.79   , 293.69   , 295.09   ],
        [289.49   , 289.49   , 290.38998, 291.59   ],
        [282.09   , 282.09   , 281.99   , 283.09   ]]], dtype=float32)
Coordinates:
  * lat      (lat) float32 20.0 30.0 40.0
    lon      (points) float32 200.0 200.0 202.5 205.0
  * time     (time) datetime64[ns] 2013-01-01 ... 2014-12-31T18:00:00
Dimensions without coordinates: points
Attributes: (11)

Warning

If an indexer is a DataArray(), its coordinates should not conflict with the selected subpart of the target array (except for the explicitly indexed dimensions with .loc/.sel). Otherwise, IndexError will be raised!

Additional Resources#

Contents