Windowed Computations

Windowed Computations#

Xarray has built-in support for windowed operations:

  1. rolling - Sliding windows of fixed length.

  2. coarsen - block windows of fixed length.

In this notebook, we’ll learn to

  1. Compute rolling, or sliding window, means along one or more dimensions.

  2. Compute block averages along a dimension.

  3. Use construct to reshape arrays so that a new dimension provides windowed views to the data.

import numpy as np
import xarray as xr
import matplotlib.pyplot as plt

np.set_printoptions(threshold=10, edgeitems=2)
xr.set_options(display_expand_data=False)

%config InlineBackend.figure_format='retina'

ds = xr.tutorial.load_dataset("ersstv5")
ds

<xarray.Dataset> Size: 40MB
Dimensions:    (lat: 89, lon: 180, time: 624, nbnds: 2)
Coordinates:
  * lat        (lat) float32 356B 88.0 86.0 84.0 82.0 ... -84.0 -86.0 -88.0
  * lon        (lon) float32 720B 0.0 2.0 4.0 6.0 ... 352.0 354.0 356.0 358.0
  * time       (time) datetime64[ns] 5kB 1970-01-01 1970-02-01 ... 2021-12-01
Dimensions without coordinates: nbnds
Data variables:
    time_bnds  (time, nbnds) float64 10kB 9.969e+36 9.969e+36 ... 9.969e+36
    sst        (time, lat, lon) float32 40MB -1.8 -1.8 -1.8 -1.8 ... nan nan nan
Attributes: (12/37)
    climatology:               Climatology is based on 1971-2000 SST, Xue, Y....
    description:               In situ data: ICOADS2.5 before 2007 and NCEP i...
    keywords_vocabulary:       NASA Global Change Master Directory (GCMD) Sci...
    keywords:                  Earth Science > Oceans > Ocean Temperature > S...
    instrument:                Conventional thermometers
    source_comment:            SSTs were observed by conventional thermometer...
    ...                        ...
    creator_url_original:      https://www.ncei.noaa.gov
    license:                   No constraints on data access or use
    comment:                   SSTs were observed by conventional thermometer...
    summary:                   ERSST.v5 is developed based on v4 after revisi...
    dataset_title:             NOAA Extended Reconstructed SST V5
    data_modified:             2022-06-07

Rolling or moving windows#

Rolling window operations

  1. can be applied along any dimension, or along multiple dimensions.

  2. returns object of same shape as input

  3. pads with NaNs to make (2) possible

Again, all common reduction operations are available

rolling = ds.rolling(time=12, center=True)
rolling

DatasetRolling [time->12(center)]

Tip

Xarrays’ computation methods (groupby, groupby_bins, rolling, coarsen, weighted) all return special objects that represent the basic underlying computation pattern. For e.g. rolling above is a DatasetRolling object that represents 12-point rolling windows of the data in ds . It is usually helpful to save and reuse these objects for multiple operations (e.g. a mean and standard deviation calculation).

ds_rolling = rolling.mean()
ds_rolling

<xarray.Dataset> Size: 40MB
Dimensions:    (time: 624, nbnds: 2, lat: 89, lon: 180)
Coordinates:
  * time       (time) datetime64[ns] 5kB 1970-01-01 1970-02-01 ... 2021-12-01
  * lat        (lat) float32 356B 88.0 86.0 84.0 82.0 ... -84.0 -86.0 -88.0
  * lon        (lon) float32 720B 0.0 2.0 4.0 6.0 ... 352.0 354.0 356.0 358.0
Dimensions without coordinates: nbnds
Data variables:
    time_bnds  (time, nbnds) float64 10kB nan nan nan nan ... nan nan nan nan
    sst        (time, lat, lon) float32 40MB nan nan nan nan ... nan nan nan nan
Attributes: (12/37)
    climatology:               Climatology is based on 1971-2000 SST, Xue, Y....
    description:               In situ data: ICOADS2.5 before 2007 and NCEP i...
    keywords_vocabulary:       NASA Global Change Master Directory (GCMD) Sci...
    keywords:                  Earth Science > Oceans > Ocean Temperature > S...
    instrument:                Conventional thermometers
    source_comment:            SSTs were observed by conventional thermometer...
    ...                        ...
    creator_url_original:      https://www.ncei.noaa.gov
    license:                   No constraints on data access or use
    comment:                   SSTs were observed by conventional thermometer...
    summary:                   ERSST.v5 is developed based on v4 after revisi...
    dataset_title:             NOAA Extended Reconstructed SST V5
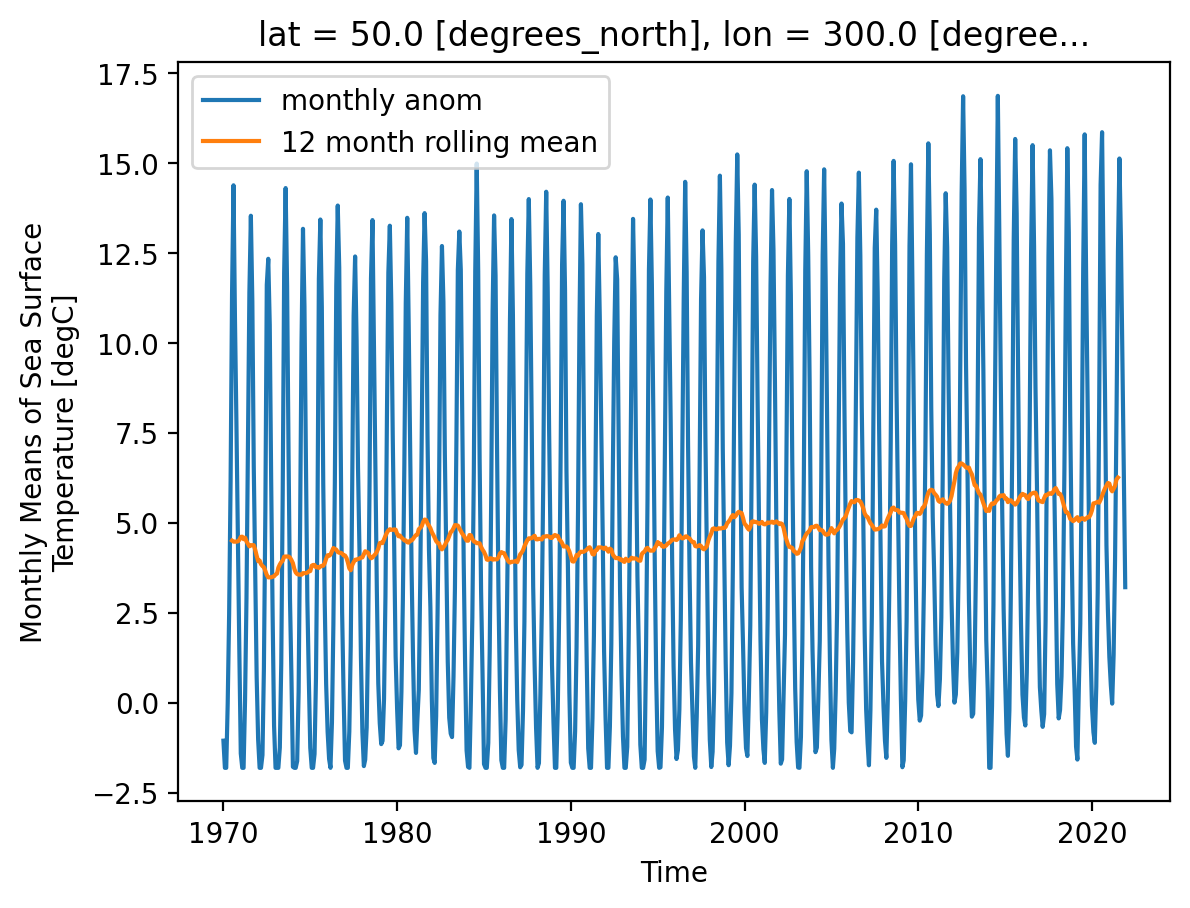
    data_modified:             2022-06-07
ds.sst.sel(lon=300, lat=50).plot(label="monthly anom")
ds_rolling.sst.sel(lon=300, lat=50).plot(label="12 month rolling mean")
plt.legend()

<matplotlib.legend.Legend at 0x7f13d0ef1e20>
../_images/60ec80a3154fe2b96c56ed71b06a97f490e25170b3e439131679b44d21acde80.png

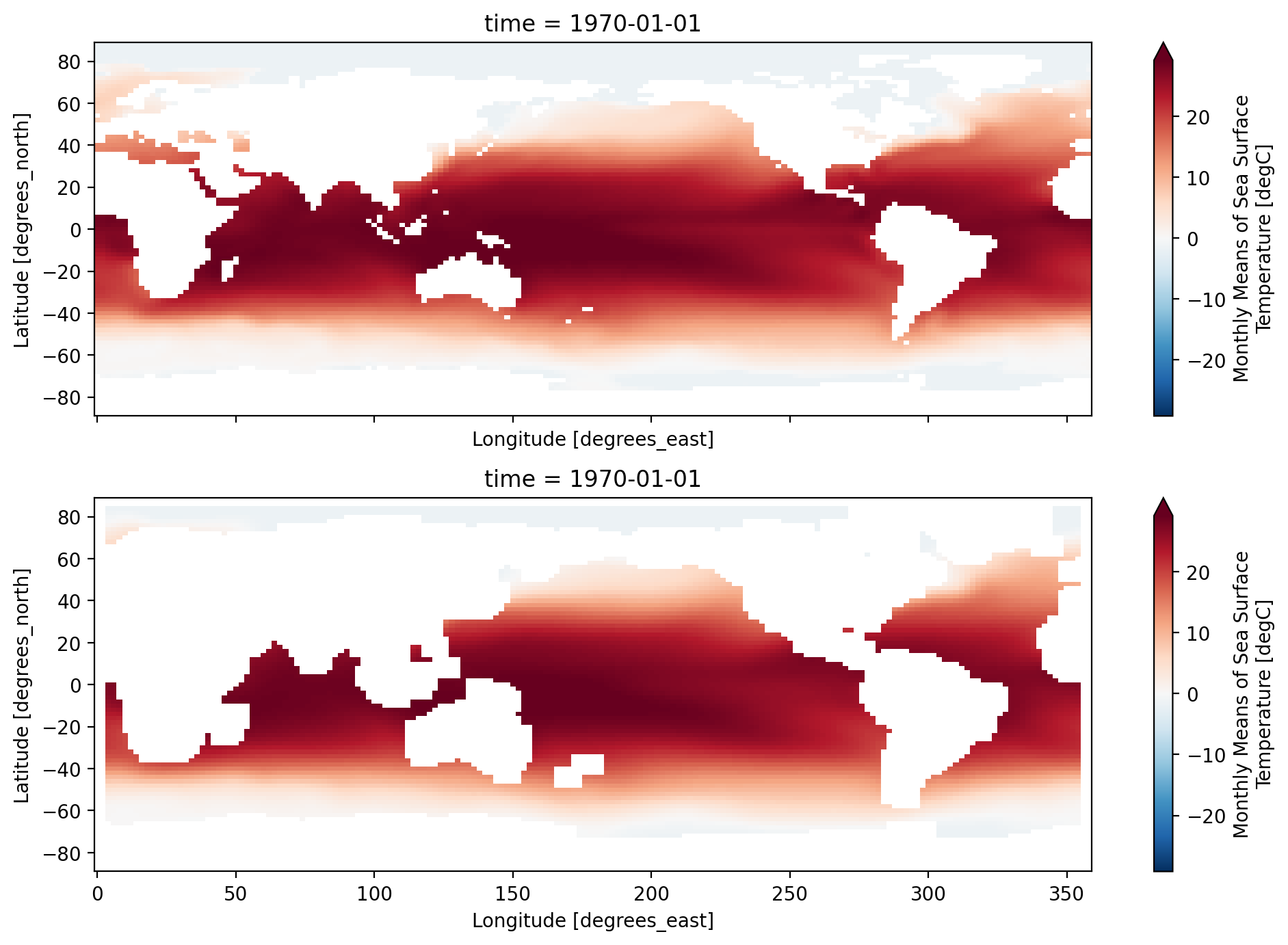
We can apply rolling mean along multiple dimensions as a 2D smoother in (lat, lon). Here is an example of a 5-point running mean applied along both the lat and lon dimensions

extract = ds.sst.isel(time=0)
smoothed = extract.rolling(lon=5, lat=5, center=True).mean()

f, ax = plt.subplots(2, 1, sharex=True, sharey=True)
extract.plot(ax=ax[0], robust=True)
smoothed.plot(ax=ax[1], robust=True)
f.set_size_inches((10, 7))
plt.tight_layout()
../_images/fb27c6d86b374f2a1b0df679980cb56f269b8ab6aa3490fa0bccc124102efc9f.png

Note the addition of NaNs at the data boundaries and near continental boundaries.

Custom reductions#

While common reductions are implemented by default, sometimes it is useful to apply our own windowed operations. For these uses, Xarray provides the construct methods for DataArray.rolling and Dataset.rolling.

For rolling over a dimension time with a window size N, construct adds a new dimension (with user-provided name) of size N.

We illustrate with a simple example array:

simple = xr.DataArray(np.arange(10), dims="time", coords={"time": np.arange(10)})
simple

<xarray.DataArray (time: 10)> Size: 80B
0 1 2 3 4 5 6 7 8 9
Coordinates:
  * time     (time) int64 80B 0 1 2 3 4 5 6 7 8 9

We call construct and provide a name for the new dimension: window

# adds a new dimension "window"
simple.rolling(time=5, center=True).construct("window")

<xarray.DataArray (time: 10, window: 5)> Size: 400B
nan nan 0.0 1.0 2.0 nan 0.0 1.0 2.0 3.0 ... 7.0 8.0 9.0 nan 7.0 8.0 9.0 nan nan
Coordinates:
  * time     (time) int64 80B 0 1 2 3 4 5 6 7 8 9
Dimensions without coordinates: window

Exercise

Illustrate the difference between center=True and center=False for rolling by looking at the construct-ed array.

Solution

display("center=True")
display(simple.rolling(time=5, center=True).construct("window"))

display("center=False")
display(simple.rolling(time=5, center=False).construct("window"))

Coarsening#

coarsen does something similar to rolling, but allows us to work with discrete non-overlapping blocks of data.

You will need to specify boundary if the length of the dimension is not a multiple of the window size (“block size”). You can choose to

  1. trim the excess values

  2. pad with NaNs

Again, all standard reductions are implemented.

coarse = ds.coarsen(lon=5, lat=5)
coarse

DatasetCoarsen [windows->{'lon': 5, 'lat': 5},side->left]

Xarrays’ computation methods (groupby, groupby_bins, rolling, coarsen, weighted) all return special objects that represent the basic underlying computation pattern. For e.g. coarse above is a DatasetCoarsen object that represents 5-point windows along lat, lon of the data in ds. It is usually helpful to save and reuse these objects for multiple operations (e.g. a mean and standard deviation calculation).

# we expect an error here because lat has size 89, which is not divisible by block size 5
coarse.mean()

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[10], line 2
      1 # we expect an error here because lat has size 89, which is not divisible by block size 5
----> 2 coarse.mean()

File ~/work/xarray-tutorial/xarray-tutorial/.pixi/envs/default/lib/python3.12/site-packages/xarray/computation/rolling.py:1339, in DatasetCoarsen._reduce_method.<locals>.wrapped_func(self, keep_attrs, **kwargs)
   1337 reduced = {}
   1338 for key, da in self.obj.data_vars.items():
-> 1339     reduced[key] = da.variable.coarsen(
   1340         self.windows,
   1341         func,
   1342         self.boundary,
   1343         self.side,
   1344         keep_attrs=keep_attrs,
   1345         **kwargs,
   1346     )
   1348 coords = {}
   1349 for c, v in self.obj.coords.items():
   1350     # variable.coarsen returns variables not containing the window dims
   1351     # unchanged (maybe removes attrs)

File ~/work/xarray-tutorial/xarray-tutorial/.pixi/envs/default/lib/python3.12/site-packages/xarray/core/variable.py:2168, in Variable.coarsen(self, windows, func, boundary, side, keep_attrs, **kwargs)
   2165 if not windows:
   2166     return self._replace(attrs=_attrs)
-> 2168 reshaped, axes = self.coarsen_reshape(windows, boundary, side)
   2169 if isinstance(func, str):
   2170     name = func

File ~/work/xarray-tutorial/xarray-tutorial/.pixi/envs/default/lib/python3.12/site-packages/xarray/core/variable.py:2204, in Variable.coarsen_reshape(self, windows, boundary, side)
   2202 if boundary[d] == "exact":
   2203     if n * window != size:
-> 2204         raise ValueError(
   2205             f"Could not coarsen a dimension of size {size} with "
   2206             f"window {window} and boundary='exact'. Try a different 'boundary' option."
   2207         )
   2208 elif boundary[d] == "trim":
   2209     if side[d] == "left":

ValueError: Could not coarsen a dimension of size 89 with window 5 and boundary='exact'. Try a different 'boundary' option.

coarse = ds.coarsen(lat=5, lon=5, boundary="trim").mean()
coarse

<xarray.Dataset> Size: 2MB
Dimensions:    (time: 624, nbnds: 2, lat: 17, lon: 36)
Coordinates:
  * lat        (lat) float32 68B 84.0 74.0 64.0 54.0 ... -46.0 -56.0 -66.0 -76.0
  * lon        (lon) float32 144B 4.0 14.0 24.0 34.0 ... 324.0 334.0 344.0 354.0
  * time       (time) datetime64[ns] 5kB 1970-01-01 1970-02-01 ... 2021-12-01
Dimensions without coordinates: nbnds
Data variables:
    time_bnds  (time, nbnds) float64 10kB 9.969e+36 9.969e+36 ... 9.969e+36
    sst        (time, lat, lon) float32 2MB -1.757 -1.78 -1.8 ... -1.685 nan
Attributes: (12/37)
    climatology:               Climatology is based on 1971-2000 SST, Xue, Y....
    description:               In situ data: ICOADS2.5 before 2007 and NCEP i...
    keywords_vocabulary:       NASA Global Change Master Directory (GCMD) Sci...
    keywords:                  Earth Science > Oceans > Ocean Temperature > S...
    instrument:                Conventional thermometers
    source_comment:            SSTs were observed by conventional thermometer...
    ...                        ...
    creator_url_original:      https://www.ncei.noaa.gov
    license:                   No constraints on data access or use
    comment:                   SSTs were observed by conventional thermometer...
    summary:                   ERSST.v5 is developed based on v4 after revisi...
    dataset_title:             NOAA Extended Reconstructed SST V5
    data_modified:             2022-06-07
coarse.sst.isel(time=0).plot();
../_images/311ce1ef24307d99bf869f10104635389bd28ee41b7a66c6ece7ec030b1adbba.png

Custom reductions#

Like rolling, coarsen also provides a construct method for custom block operations.

Tip

coarsen.construct is a handy way to reshape Xarray objects.

Consider a “monthly” 1D timeseries. This simple example has one value per month for 2 years

months = xr.DataArray(
    np.tile(np.arange(1, 13), reps=2),
    dims="time",
    coords={"time": np.arange(1, 25)},
)
months

<xarray.DataArray (time: 24)> Size: 192B
1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12
Coordinates:
  * time     (time) int64 192B 1 2 3 4 5 6 7 8 9 ... 16 17 18 19 20 21 22 23 24

Now we reshape to get one new dimension year of size 12.

# break "time" into two new dimensions: "year", "month"
months.coarsen(time=12).construct(time=("year", "month"))

<xarray.DataArray (year: 2, month: 12)> Size: 192B
1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12
Coordinates:
    time     (year, month) int64 192B 1 2 3 4 5 6 7 8 ... 18 19 20 21 22 23 24
Dimensions without coordinates: year, month

Exercise

Imagine the array months was one element shorter. Use boundary="pad" and the side kwarg to reshape months.isel(time=slice(1, None)) to a 2D DataArray with the following values:

array([[nan,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10., 11., 12.],
       [ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10., 11., 12.]])

Solution

months.isel(time=slice(1, None)).coarsen({"time": 12}, boundary="pad", side="right").construct(
    time=("year", "month")
)

Note that coarsen pads with NaNs. For more control over padding, use DataArray.pad explicitly.

Going further#

  1. See the documentation on rolling and coarsen.

  2. Follow the tutorial on high-level computational patterns

Contents